Portes logiques de base et expressions booléennes
2024-05-10
9920
Dans le domaine de l'électronique numérique, la compréhension des concepts de base des portes logiques et des expressions booléennes est primordiale pour les ingénieurs en herbe et assaisonnés.Cet article plonge dans les principes fondamentaux des portes logiques, qui sont les principales composantes des circuits numériques, jetant les bases des processus de prise de décision binaires qui sous-tendent l'informatique moderne.Les portes logiques manipulent les signaux binaires basés sur les règles de l'algèbre booléenne, un cadre critique utilisé pour simplifier et analyser la logique des circuits numériques.Ces portes, construites principalement à partir de transistors, traduisent les entrées électriques en sorties binaires - des niveaux élevés ou de faible tension, correspondant aux valeurs binaires de 1 et 0, respectivement.Ce document explore les principes opérationnels, les représentations symboliques et les applications pratiques de divers types de portes logiques telles que non, et, ou, XOR, NAND, et ni, chacune caractérisée par des fonctionnalités distinctes et instrumentale dans l'élaboration de la logique complexe complexe.
Catalogue

Figure 1: Symboles graphiques du circuit de porte logique de base
Présentation de la porte logique
Les portes logiques sont des blocs de construction fondamentaux dans les circuits intégrés, principalement construits à partir de transistors.Chaque porte combine des transistors d'une manière spécifique pour manipuler les signaux électriques.Au fur et à mesure que les signaux passent à travers ces portes, ils émergent comme des niveaux élevés ou faibles - transformant essentiellement l'entrée électrique en une sortie binaire.Ces états élevés et bas correspondent à des valeurs binaires de 1 et 0 ou logiques "vrai" et "false".Cette transformation est la base pour effectuer des opérations logiques.
Les types les plus courants de portes logiques sont les non, et, ou, XOR, NAND et NOR GATES.Chaque porte fonctionne uniquement:
Une porte non prend une seule entrée et l'inverse;Si l'entrée est élevée, la sortie est faible et vice versa;
AN et Gate ne produit un signal élevé que si toutes ses entrées sont élevées;
Une porte ou une sortie fournit une sortie élevée si au moins une entrée est élevée;
Une porte XOR fournit une sortie élevée uniquement lorsqu'un nombre impair de ses entrées est élevé;
Une porte NAND est similaire à une porte et produit un signal faible si toutes ses entrées sont élevées;
Une porte NOR fonctionne comme une porte ou donne une sortie faible si une entrée est élevée.
En combinant ces portes dans diverses configurations, des fonctions logiques plus complexes peuvent être exécutées, facilitant les opérations sophistiquées et les processus de prise de décision dans les ordinateurs et autres appareils numériques.Chaque porte logique joue un grand rôle dans la façon dont les systèmes numériques traitent les informations et effectuent des calculs.
Pas la porte
La porte non, communément appelée onduleur, est une composante fondamentale dans les circuits numériques.Sa conception comprend une entrée et une extrémité de sortie, la sortie est généralement marquée par un cercle indiquant l'inversion du signal.Cette configuration simple permet à la porte non inversée de son entrée: un signal élevé (logique "true") devient faible (logique "false"), et vice versa.

Figure 2: Les 3 symboles des portes logiques
En termes de symboles, la porte non représentée est représentée différemment entre diverses normes.L'ANSI / IEEE STD 91-1984 utilise des symboles caractéristiques de forme, tandis que l'IEC 60617-12 utilise des symboles standard nationaux rectangulaires.Bien qu'il ne soit plus utilisé, le DIN 40700 a fourni un autre ensemble de symboles historiquement.
En se concentrant sur son application, la porte NON sert de bloc de construction critique dans les circuits numériques.Une utilisation courante consiste à créer un verrou.Cela se fait en connectant les sorties de deux onduleurs séquentiels aux entrées d'un registre à un bits, formant un élément de mémoire de base.Un exemple d'application pratique de non-portes est le Hexa-Inverter, un circuit intégré qui contient six onduleurs individuels.Par exemple, la puce 7404 TTL et la puce 4049 CMOS intègrent toutes deux six onduleurs.Ces puces sont conçues avec 14 et 16 broches respectivement, y compris deux broches pour la tension d'alimentation / référence et les broches restantes dédiées aux onduleurs, bien que la puce 4049 ait deux broches qui ne sont pas connectées.
Et porte
La porte et une composante fondamentale des circuits numériques, sont souvent mentionnées par plusieurs noms, notamment "et circuit", logique "produit" et logique "et" circuit.Il fonctionne en effectuant une opération "et", ce qui signifie qu'il nécessite plusieurs entrées et produit une sortie.La sortie d'une porte et de la porte ne fait que haut (logique 1) lorsque toutes ses entrées sont simultanément élevées.Si une entrée est faible (logique 0), la sortie sera également faible.Cette opération peut être exprimée mathématiquement en y = a × b.
En termes de symboles, la porte et la porte est représentée de plusieurs manières selon les différentes normes: le symbole caractéristique de forme selon ANSI / IEEE STD 91-1984, le symbole standard national rectangulaire IEC (IEC 60617-12), et le symbole DIN plus ancien(DIN 40700).
Et les portes peuvent être implémentées à l'aide de diverses technologies, notamment des CMO, des NMO, des PMO et de la logique basée sur les diodes.Cette polyvalence permet à des portes et des portes dans les circuits intégrés TTL (Transistor-Transistor Logic) et CMOS (CMOS (complémentaire-oxyde-semi-conducteur), ce qui les rend intégrales à l'électronique moderne.
La mise en œuvre et les portes dans les circuits intégrés est répandue.Par exemple, les circuits CMOS de série 74 standard comprennent:
74x08 et 74x09 (OC), contenant chacun quatre entrées indépendantes à 2 entrées et portes;
74x11, qui comprend trois entrées indépendantes et des portes;
74x21, qui comprend deux entraves indépendantes et des portes.
De même, la série CD4000 de circuits intégrés, une autre famille commune, contient:
CD4081, avec quatre entrées de 2 et portes,
CD4082, qui comprend deux entraves et les portes.
Ces circuits intégrés sont généralement utilisés dans divers appareils numériques où le contrôle logique précis et la prise de décision basés sur plusieurs conditions sont nécessaires.Chaque type de circuit offre une configuration spécifique d'entrées, permettant des applications flexibles et personnalisées dans les systèmes numériques.

Figure 3: 74x21

Figure 4: CD4081
Ou porte
La porte OR, également appelée «ou circuit», est un élément crucial dans la logique numérique où il évalue plusieurs conditions.Si au moins une condition est remplie, c'est-à-dire si au moins une des entrées de la porte OR est élevée (logique 1) - la sortie est définie élevée (logique 1).Inversement, la sortie est faible (logique 0) uniquement lorsque toutes les entrées sont faibles.Cette logique binaire constitue la base de la relation "ou" logique, qui stipule que la survenue d'un événement dépend de la satisfaction de l'une des nombreuses conditions.
En termes pratiques, ou les portes sont largement utilisées dans les circuits numériques pour gérer les décisions qui nécessitent au moins l'une des nombreuses entrées pour être vraies.Par exemple, une porte ou une porte peut contrôler un mécanisme qui s'active si l'un des nombreux capteurs est déclenché.Ces portes peuvent être combinées pour gérer des arrangements d'entrée plus complexes.Par exemple, plusieurs entraves ou portes peuvent être liées pour étendre le nombre de conditions qu'ils traitent, améliorant leur utilité dans des conceptions de circuits plus complexes.
Passer à la porte XOR, ce composant sert une fonction spécifique dans la logique numérique en implémentant les opérations XOR logiques.La porte XOR a deux bornes d'entrée et une borne de sortie.Il offre une sortie élevée (logique 1) lorsque les niveaux d'entrée diffèrent et une sortie faible (logique 0) lorsque les entrées sont les mêmes.Cette fonctionnalité unique permet à la porte XOR d'effectuer des ajout de modulo 2, ce qui est fondamental dans le calcul de l'ajout binaire.
La capacité de la porte XOR à différencier les états d'entrée identiques et différents est particulièrement utile dans les circuits arithmétiques, tels que la demi-ajout.Un demi-ajout, qui ajoute deux chiffres binaires uniques, est construit à l'aide d'une porte XOR et d'un et de la porte.La porte XOR gère l'opération de sommation, tandis que la porte et détermine s'il y a un report vers le bit supérieur suivant.L'expression logique pour une opération XOR est représentée comme 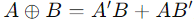 .
.
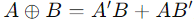 .
.
Figure 5: Gate XOR
Porte nand
La porte NAND est essentiellement une combinaison d'une porte et d'une porte non, conçue pour effectuer les deux opérations séquentiellement.Il commence par une opération et une opération, prenant deux entrées, puis applique une opération non pas au résultat.La dynamique de la porte NAND est simple: si les deux entrées sont élevées (les deux à la logique 1), la sortie est faible (logique 0).Cependant, si une entrée est faible (logique 0), la sortie est élevée (logique 1).Cette inversion de la sortie et de la porte fait de la porte NAND un composant critique dans les circuits numériques.L'expression logique pour une porte NAND est 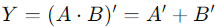 , mettant en évidence l'inversion après l'opération et.
, mettant en évidence l'inversion après l'opération et.
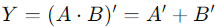 , mettant en évidence l'inversion après l'opération et.
, mettant en évidence l'inversion après l'opération et.
Figure 6: Nand Gate Truth Table
Dans les scénarios pratiques, comme dans les circuits de porte NAND DTL (diode-transistor), la combinaison de la diode et des portes et du transistor et non des portes est courante.Ces configurations visent à gérer les écarts de niveau qui se produisent lorsque les portes sont connectées en série et à améliorer la capacité de charge.Les composants de ces circuits - diodes, transistors, résistances et fils de connexion - sont généralement intégrés dans une puce à semi-conducteur, formant ce qui est connu comme un circuit intégré.
Les circuits DTL, malgré leur structure simple, sont tombés en disgrâce en raison de leurs vitesses opérationnelles lentes.D'un autre côté, les circuits TTL (transistor-transistor), qui sont des modifications de DTL, continuent d'être largement utilisés.Ces améliorations incluent la conception de l'étape d'entrée, où un transistor multi-émetteur remplace une diode et une porte simples pour améliorer les vitesses de commutation.Cette disposition permet une amplification plus efficace, fournissant un courant de base inverse plus fort pour effacer rapidement la charge de stockage en excès lorsque le transistor est saturé, ce qui améliore considérablement la vitesse de désactivation.Pour augmenter la vitesse d'activation du transistor de sortie, une diode dans le
Le circuit peut être remplacé par un transistor qui maintient la logique
relations tout en améliorant l'amplification pendant les circuits
Activation.Cela aide à fournir un courant de base plus grand à la sortie
transistor, accélérant son activation.Enfin, l'étape de sortie est conçue pour avoir une capacité de charge robuste.
Ceci est réalisé en remplaçant la résistance de charge de collection traditionnelle
avec une charge active composée de transistors et résistances supplémentaires.
Cette configuration push-pull, entraînée par deux signaux complémentaires,
s'assure qu'un transistor est toujours allumé pendant que l'autre est éteint,
maintenir un fonctionnement stable et efficace.
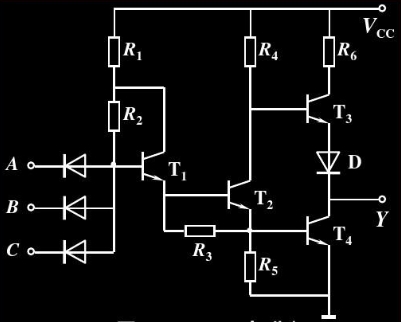
Figure 7: circuit de porte DTL NAND
Ni Gate
La porte NOR est conçue pour effectuer la fonction logique ni fonction.Il a généralement plusieurs entrées mais une seule sortie.Une porte NOR fonctionne de telle sorte qu'il délivre une sortie élevée (logique 1) uniquement si toutes ses entrées sont faibles (logique 0).Si une entrée est élevée (logique 1), la sortie passe immédiatement à faible (logique 0).Ce comportement résume l'opération NOR, ce qui en fait une porte universelle qui peut être utilisée pour implémenter d'autres fonctions logiques de base comme et, ou non via diverses combinaisons et configurations.

Figure 8: Nor Gate IEC 60617-12

Figure 9: CMOS Logic
La polyvalence de la porte NOR se reflète dans sa capacité à créer des fonctions logiques complexes seule.Cette caractéristique unique est symbolisée par les normes ANSI / IEEE STD 91-1984 et IEC 60617-12, qui fournissent des représentations graphiques distinctes pour ces portes.La norme ANSI / IEEE utilise des symboles caractéristiques de forme, tandis que la norme IEC utilise des symboles rectangulaires.Les portes ni les composantes fondamentales ne sont ni dans les circuits TTL (logique de transistor-transistor) et CMOS (semi-conducteur d'oxyde métallique complémentaire).Ils sont particulièrement répandus dans les puces logiques standard:

Figure 10: via Nand Gate

Figure 11: CD4001
Dans la série CMOS 4000, le CD4000 dispose de deux portes à 3 entrées et d'une seule porte non pas, le CD4001 comprend quatre portes à 2 entrées ni des portes, et le CD4002 abrite deux portes à 4 entrées ni portes.

Figure 12: CD4000

Figure 13: CD4002
Dans la série TTL 74, le 74x02 propose quatre portes à 2 entrées, le 74x27 contient trois portes à 3 entrées, et le 7428 fournit deux portes à 4 entrées.

Figure 14: 74x02

Figure 15: 74x27
Expression booléenne
Une expression booléenne dans la programmation évalue à l'une des deux valeurs possibles: vrai ou faux.À son plus simple, une expression booléenne vérifie si une valeur équivaut à une autre, comme dans l'expression '2 == 4'.Cette expression évalue à FAUX car 2 ne correspond pas aux expressions booléennes plus complexes, telles que , s'appuie sur l'état d'exécution pour l'évaluation et peut produire vrai ou faux en fonction des valeurs actuelles des propriétés des objets.
, s'appuie sur l'état d'exécution pour l'évaluation et peut produire vrai ou faux en fonction des valeurs actuelles des propriétés des objets.
 , s'appuie sur l'état d'exécution pour l'évaluation et peut produire vrai ou faux en fonction des valeurs actuelles des propriétés des objets.
, s'appuie sur l'état d'exécution pour l'évaluation et peut produire vrai ou faux en fonction des valeurs actuelles des propriétés des objets.Dans les langages de programmation comme C, C ++ et C #, il est important de faire la distinction entre '==', l'opérateur d'égalité utilisé dans les expressions booléennes pour comparer les valeurs, et '=', l'opérateur d'affectation utilisé pour définir une variable sur une valeur.La mauvaise utilisation de ces opérateurs peut entraîner des erreurs lors de la compilation du programme ou pendant son exécution.Les expressions booléennes sont construites à l'aide d'opérandes booléens et d'opérateurs logiques, adhérant à des règles de syntaxe spécifiques.Les opérateurs comprennent:
Logique et (∧)
Logique ou (∨)
Logique pas (¬)
Dans certains contextes de programmation, des opérateurs supplémentaires comme l'équivalence (≡) et implication (→) sont également utilisés.Ces expressions peuvent contenir des variables booléennes, des expressions relationnelles (des comparaisons comme moins que ou supérieures à) et d'autres expressions booléennes encapsulées entre parenthèses.La valeur vraie ou fausse d'une expression relationnelle (par exemple, e1 < E2) is determined by the comparison of E1 and E2, which are arithmetic expressions. If E1 is indeed less than E2, the expression evaluates to true, otherwise false. In programming, Boolean expressions serve two primary functions:they are used as conditions to control the flow in various control structures and they can compute logical values directly. The precedence of operations in Boolean expressions typically follows this order:
Parenthèses
Opérateurs arithmétiques (*, /, +, -,%)
Opérateurs relationnels (<, <=, =, >,> =, <>)
Opérateurs logiques (¬, ∧, ∨)
Pour plus d'efficacité dans l'évaluation, toute l'expression booléenne entière n'a pas besoin d'être évaluée.Par exemple, dans l'expression «a ∨ b», si A est vrai, l'expression entière est vraie indépendamment de B. Ce concept introduit l'idée de «court-circuit», où l'évaluation peut s'arrêter tôt si le résultat est déjà déterminépar une partie de l'expression.Dans des expressions booléennes complexes comme «a∨ (b∧ (¬c∨d)», l'utilisation d'évaluation structurée peut conduire à une génération de code intermédiaire plus efficace, souvent utilisée dans la conception du compilateur.Selon les valeurs de «A», «B», «C» et «D», le chemin et le résultat de l'évaluation peuvent varier, mettant en évidence les points de l'expression qui déterminent de manière décisive son résultat - ont été «sortis».Ces sorties indiquent la direction du flux de contrôle dans les processus de calcul, guidant si le contrôle doit se dérouler comme si la valeur booléenne était évaluée comme vraie ou fausse.Ce mécanisme est essentiel dans la conception des structures de contrôle dans la programmation, permettant des chemins d'exécution dynamiques et conditionnels basés sur la logique booléenne.
Déterminant la valeur de vérité d'une expression booléenne, E est un processus méthodique qui se déroule pendant la traduction de la grammaire.Considérons une expression comme «e = e (1) ∨ e (2)».Si E (1) évalue à True, alors l'expression entière «E» est vraie, ce qui signifie que le vrai point de terminaison de «E (1)» est également un véritable point de terminaison pour «E».Cependant, si «e (1)» est faux, la valeur de E dépend alors de «e (2)».Dans ce scénario, «E (2)» doit être évalué ensuite.Le faux critère d'évaluation de «E (1)» nous dirige vers le début de «E (2)», et les résultats vrais et faux de «E (2)« Définissez les résultats correspondants pour «E».
Dans la création d'un algorithme de traduction d'expression booléen, plusieurs types de quaternions de contrôle sont utilisés:
(Jnz, A1, P) - Si «A1» est vrai (non nul), il passe au Quaternion p.
(Jrop, A1, A2, P) - saute au quaternion p si la relation «a1 rop a2» est vraie.
(J ,,, P) - saute inconditionnellement à Quaternion p.
Par exemple, dans l'énoncé conditionnel «Si A ∨ B < C then S1 else S2', the translated quaternion sequence might look like this:
(Jnz, A, -, 5) - Si A est vrai, sautez directement à l'action pour S1.
(J, -, -, 3) - Un saut inconditionnel pour évaluer «B» < 'C'.
(J <, B, C, 5) - Si b < C is true, jump to execute S1.
(J, -, -, P + 1) - suivi de la séquence de quaternion pour S1.
(p) (j, -, -, q) - suit l'exécution de S2 après S1 ou si ni un ni b < C is true.
Dans la traduction ascendante guidée par grammaire, lorsqu'un quaternion de contrôle est créé, le quaternion cible pourrait ne pas exister, conduisant à des transferts de contrôle initialement incomplets.Par exemple, '(jnz, a, -, 0)' pourrait être généré avec un espace réservé parce que le véritable point de terminaison d'un (ou le point de départ pour S1) n'est pas encore connu.Cet placeholder est mis à jour lorsque la destination devient claire.Pendant la traduction, il est courant que plusieurs quaternions pointent vers une cible non encore déterminée.Ceux-ci sont liés ensemble et mis à jour une fois la cible définie.Dans cette traduction guidée par syntaxe, il est utile de reformater la grammaire pour s'assurer que les attributs sémantiques comme les chaînes de sortie vraies et fausses (TC et FC) sont capturées en temps opportun:
Qexpr®Expr ∧ Expr |Expr ∨ expr |¬ expr |iden |iden rop iden |(Expr)
Expr ∧ ® expr ∧
Expr ∨ ® expr ∨
Cette «division» de la grammaire permet un accès immédiat au TC et au FC des expressions à gauche d'un opérateur;Une fois ces attributs connus, ils peuvent être utilisés pour remplir le TC ou FC respectif de l'expression antérieure en utilisant le prochain numéro de quaternion disponible.Cette approche structurée est vitale pour gérer efficacement les structures de contrôle complexes dans la programmation, où la précision logique dicte le flux et le fonctionnement du programme, un peu comme les portes logiques contrôlent les circuits électriques.
Conclusion
La danse complexe des portes logiques et des expressions booléennes forme l'épine dorsale de la conception de la logique numérique, permettant la construction de dispositifs et de systèmes électroniques sophistiqués.Grâce à l'exploration détaillée de la fonctionnalité de chaque porte et de son rôle dans des circuits plus grands, cet article illumine la façon dont les décisions binaires simples dégénèrent en opérations de calcul complexes.L'exploration d'applications pratiques, des éléments de mémoire de base aux circuits intégrés avancés, met en évidence la polyvalence et la nature essentielle de ces composants dans la technologie moderne.En intégrant les connaissances théoriques aux applications pratiques, l'étude des portes logiques et des expressions booléennes enrichit non seulement des activités académiques et professionnelles, mais propulse également le domaine de l'électronique numérique.
Questions fréquemment posées [FAQ]
1. Quelle est la différence entre une porte logique et une expression booléenne?
Une porte logique est un appareil physique (ou un modèle dans une conception de circuit) qui effectue une opération logique sur une ou plusieurs entrées binaires pour produire une seule sortie, en fonction de certaines règles.Il est généralement représenté dans le matériel par des transistors dans les circuits numériques.
Une expression booléenne, en revanche, est une expression mathématique qui évalue à l'une des deux valeurs, vraies ou fausses.Les expressions booléennes utilisent des opérateurs logiques et sont utilisés dans la programmation et l'informatique théorique pour décrire les opérations logiques algébriquement.
2. Quelles sont les 7 portes logiques?
Et Gate: les sorties ne sont vraies que si toutes les entrées sont vraies.
Ou porte: sorties True si au moins une entrée est vraie.
Pas de porte (onduleur): sortit l'opposé de l'entrée.
NAND GATE: Sorties Faux uniquement si toutes les entrées sont vraies.
Ni Gate: Sorties True uniquement si toutes les entrées sont fausses.
XOR Gate (exclusif ou): Sorties True si les entrées sont différentes.
XNOR GATE (exclusif NOR): Sorties True si les entrées sont les mêmes.
3. Qu'est-ce qu'un exemple d'expression booléenne?
Un exemple d'expression booléenne est «a et non b».Cette expression évalue à la vraie que si A est vrai et B est faux.En termes logiques, il peut être écrit comme «a∧¬b».
4. Quels sont les trois types de portes logiques?
Si par «types», vous voulez dire des classes basées sur les fonctionnalités, les trois catégories de base de portes logiques incluent:
Portes de base: et, ou non
Portes universelles: nand ou (peut être utilisée pour construire tout autre type de porte)
Gates spécialisées: xor, xnor (utilisé pour des fonctions spécifiques comme la vérification et l'égalité de la parité)
5. Comment identifier les portes logiques?
Les portes logiques peuvent être identifiées par leurs symboles et tables de vérité:
Chaque porte a un symbole distinct, par exemple, et les portes sont dessinées comme en forme de D avec une ligne sur le côté plat, ou les portes sont incurvées à un point à la sortie.Examinez le tableau qui répertorie les possibilités d'entrée et les sorties correspondantes.Par exemple, le tableau de vérité et la porte ne montrera qu'une sortie élevée (1) lorsque toutes ses entrées sont élevées (1).
Pour augmenter la vitesse d'activation du transistor de sortie, une diode dans le
Le circuit peut être remplacé par un transistor qui maintient la logique
relations tout en améliorant l'amplification pendant les circuits
Activation.Cela aide à fournir un courant de base plus grand à la sortie
transistor, accélérant son activation.
Pour augmenter la vitesse d'activation du transistor de sortie, une diode dans le
Le circuit peut être remplacé par un transistor qui maintient la logique
relations tout en améliorant l'amplification pendant les circuits
Activation.Cela aide à fournir un courant de base plus grand à la sortie
transistor, accélérant son activation.
 À PROPOS DE NOUS
Satisfaction client à chaque fois.Confiance mutuelle et intérêts communs.
À PROPOS DE NOUS
Satisfaction client à chaque fois.Confiance mutuelle et intérêts communs.
test de fonctionnalité.Les produits les plus rentables et le meilleur service sont notre engagement éternel.
Article chaud
- Sont CR2032 et CR2016 interchangeables
- MOSFET: Définition, principe de travail et sélection
- Installation et test de relais, interprétation des schémas de câblage de relais
- CR2016 contre CR2032 Quelle est la différence
- NPN contre PNP: Quelle est la différence?
- ESP32 vs STM32: Quel microcontrôleur est meilleur pour vous?
- LM358 Double amplificateur opérationnel Guide complet: broches, diagrammes de circuits, équivalents, exemples utiles
- CR2032 VS DL2032 VS CR2025 Guide de comparaison
- Comprendre les différences ESP32 et ESP32-S3 Analyse technique et de performance
- Analyse détaillée du circuit de la série RC
 Exploration de la fonctionnalité et de la conception de résistances dépendantes de la lumière
Exploration de la fonctionnalité et de la conception de résistances dépendantes de la lumière
2024-05-10
 Comprendre les différences ESP32 et ESP32-S3 Analyse technique et de performance
Comprendre les différences ESP32 et ESP32-S3 Analyse technique et de performance
2024-05-09
Numéro de pièce chaud
 GRM32NR71C335KA01L
GRM32NR71C335KA01L 12101C684KAT2A
12101C684KAT2A GRM0335C1H6R7CA01D
GRM0335C1H6R7CA01D 02013A1R5CAT2A
02013A1R5CAT2A GRM3166R1H241JZ01D
GRM3166R1H241JZ01D T491D226K025AH
T491D226K025AH Q8025L6TP
Q8025L6TP MPQ3906
MPQ3906 ZXMN2088DE6TA
ZXMN2088DE6TA MAX1137EUA+T
MAX1137EUA+T
- MC9S08GT8ACFBER
- ZLP12840H2864G
- MAX4066AESD
- EL1508CL
- CY7C1312KV18-250BZXC
- AC0805FR-0751RL
- 7MBP100RA060
- CD4066BNSR
- BC107B
- ADS1222IPWR
- AD9042ASTZ
- PM8043B-F3EI
- HMC1010LP4ETR
- LM4030CMF-4.096/NOPB
- ADV7123KST140
- BQ2058-C
- CY62147DV30LL-70BVIT
- LAN91C96
- LM25575QMHX
- MACH110-12JC-14JI
- MAX5160LEUA-T
- MB90F372
- MC14052BF12
- MN102L62GCK
- MT46H16M32LFCX-6IT:B
- OPA3690IDBQRG4
- RTC8583A
- SL28506AZC-3T
- ST32F051C8T6
- ST32F100C6T6B
- AN3117S-CE1
- MT42L128M64D2MP-25WT:A
- SM8770CT-G-ET
- SRM2264LTM90
- SAK-XC2361E-104F128L-AA
- AK5366VR-L
- BCM8742BKFBG
- EMMC64G-M525-A52
- XCZU27DR-2FFVE1156I