Analyse détaillée du circuit de la série RC
2024-05-08
20520
Le circuit de la série RC, composé d'une résistance et d'un condensateur, sert de composant fondamental dans les conceptions de système électronique de base et avancées.Il aide à comprendre les principes clés tels que la réponse en fréquence, le décalage de phase et le filtrage du signal, qui jouent un rôle important dans la conception des circuits et le traitement du signal.Cette exploration couvre les bases théoriques et s'étend à des applications pratiques à travers des expériences et des simulations.En assemblant physiquement le circuit ou en le modélisant numériquement, les apprenants peuvent saisir visuellement le processus de charge et les effets des ions composante V ariat, ce qui rend les concepts complexes plus accessibles et mémorables.
Catalogue
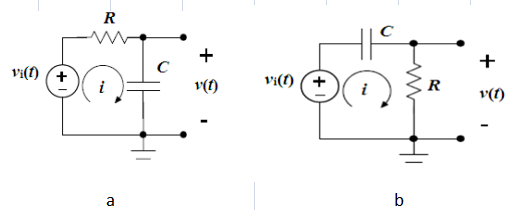
Figure 1: Différentes tensions de sortie des circuits RC
Introduction au circuit RC
Un circuit RC, abréviation du circuit de capacité de résistance, est fondamental en électronique pour manipuler les signaux par des résistances et des condensateurs.Ces circuits sont particulièrement connus pour leur capacité à déplacer les phases et à filtrer les signaux, en utilisant des arrangements simples de ces composants.Un circuit RC de base, souvent appelé circuit RC de premier ordre, comprend généralement une seule résistance et un condensateur.
Dans une configuration typique, la tension d'entrée est appliquée à la disposition série d'une résistance et d'un condensateur.La sortie peut être dessinée à travers la résistance ou le condensateur, chacune donnant des réponses différentes aux fréquences du signal en raison des caractéristiques uniques du condensateur.Cette polyvalence permet aux circuits RC d'obtenir une variété de rôles dans des appareils électroniques, tels que le couplage et le filtrage des signaux ou même la conversion des formes d'onde lorsqu'elles sont soumises en une tension de pas.
Le circuit RC peut être configuré de plusieurs manières: séries, parallèles ou une combinaison des deux, appelés séries parallèles.Chaque configuration affecte les fréquences du signal différemment: les connexions en série ont tendance à atténuer les basses fréquences, tandis que les connexions parallèles sont utilisées pour atténuer les fréquences plus élevées.Cette différence est principalement due à la façon dont les résistances et les condensateurs interagissent avec le circuit;Les résistances s'opposent directement au courant tandis que les condensateurs le stockent et la relâchent, ce qui a un impact sur la façon dont le circuit réagit à différentes fréquences.
Contrairement aux circuits qui incluent des inductances, comme les circuits LC, les circuits RC simples ne peuvent pas résonner car les résistances ne stockent pas l'énergie.Cet attribut influence distinctement la façon dont les circuits RC sont utilisés, en se concentrant sur leur capacité de filtrage plutôt que sur le stockage ou la résonance d'énergie.Chaque configuration sert un objectif spécifique, faisant des circuits RC outils polyvalents dans une étude théorique et une application pratique dans la conception électronique.
Circuit de la série RC
Un circuit de la série RC, essentiellement composé d'une résistance (R) et un condensateur (C) En série, fonctionne sur un principe simple.Lorsque l'interrupteur du circuit est fermé, le condensateur commence à se charger de la tension appliquée (V), initiant un flux de courant à travers le circuit.À mesure que le condensateur charge, le courant augmente progressivement jusqu'à ce que le condensateur atteigne sa capacité, à quel point il cesse d'accepter les charges, et le courant se stabilise à sa valeur maximale, calculé comme 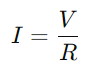 .
.
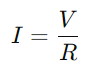 .
.Le processus de charge du condensateur peut être décrit mathématiquement par l'équation 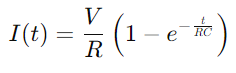 , où je suis le courant, V est la tension, R est la résistance, C est la capacité, t est le temps, et e est la base du logarithme naturel.Cette formule reflète comment le courant change avec le temps lorsque le condensateur charge, avec le produit des valeurs de résistance et de capacité (RC) définissant la constante de temps du circuit, indiquant la vitesse à laquelle le condensateur charge.
, où je suis le courant, V est la tension, R est la résistance, C est la capacité, t est le temps, et e est la base du logarithme naturel.Cette formule reflète comment le courant change avec le temps lorsque le condensateur charge, avec le produit des valeurs de résistance et de capacité (RC) définissant la constante de temps du circuit, indiquant la vitesse à laquelle le condensateur charge.
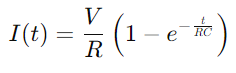 , où je suis le courant, V est la tension, R est la résistance, C est la capacité, t est le temps, et e est la base du logarithme naturel.Cette formule reflète comment le courant change avec le temps lorsque le condensateur charge, avec le produit des valeurs de résistance et de capacité (RC) définissant la constante de temps du circuit, indiquant la vitesse à laquelle le condensateur charge.
, où je suis le courant, V est la tension, R est la résistance, C est la capacité, t est le temps, et e est la base du logarithme naturel.Cette formule reflète comment le courant change avec le temps lorsque le condensateur charge, avec le produit des valeurs de résistance et de capacité (RC) définissant la constante de temps du circuit, indiquant la vitesse à laquelle le condensateur charge.
Figure 2: circuit de la série RC
La décharge se produit lorsque l'interrupteur est ouvert, inversant le processus: l'énergie stockée dans le condensateur est libérée, ce qui fait couler le courant dans la direction opposée jusqu'à ce que le condensateur soit drainé.Ce cycle de charge et de décharge est crucial dans des applications telles que la conversion du signal, le filtrage et les circuits de synchronisation en raison de la manière prévisible dont le courant et la tension changent.
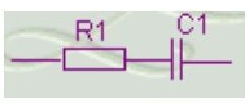
Figure 3: court-circuit de la série RC
Le comportement du circuit de la série RC varie également avec la fréquence.À basse fréquence, le condensateur agit davantage comme un circuit ouvert, entravant considérablement l'écoulement du courant.À mesure que la fréquence augmente, la réactance capacitive diminue, ce qui facilite le passage du courant.Ce changement d'impédance avec la fréquence permet au circuit de la série RC d'agir comme un filtre, atténuant sélectivement les fréquences inférieures à un certain seuil (fréquence de virage 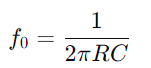 ).
).
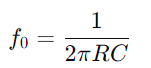 ).
).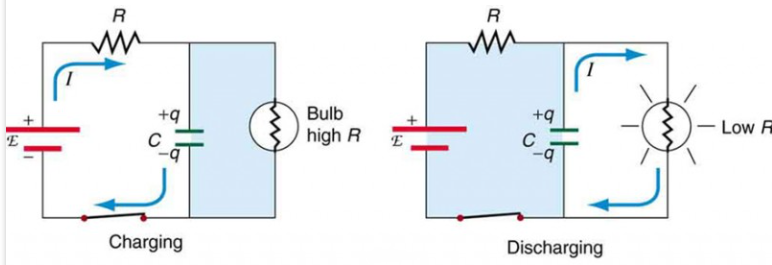
Figure 4: Charge et décharge des circuits de la série RC
En plus des opérations à l'état d'équilibre, les circuits RC sont également étudiés pour leurs réponses transitoires lorsqu'elles sont soumises à des changements soudains de tension, comme lorsqu'une alimentation CC est activée ou désactivée.Ce scénario est appelé un processus transitoire, où le circuit passe d'un état stable à un autre.La dynamique de ce processus dépend considérablement de la constante de temps RC, qui régit la rapidité avec laquelle le circuit réagit aux changements.
En fin de compte, les circuits de la série RC remplissent plusieurs fonctions dans les applications DC et AC, gérant les tâches allant du retard des signaux à l'intégration ou au couplage de divers éléments de circuit.Cette polyvalence découle des interactions uniques entre la résistance et le condensateur, qui déterminent ensemble la réponse globale du circuit aux changements de tension et de fréquence.
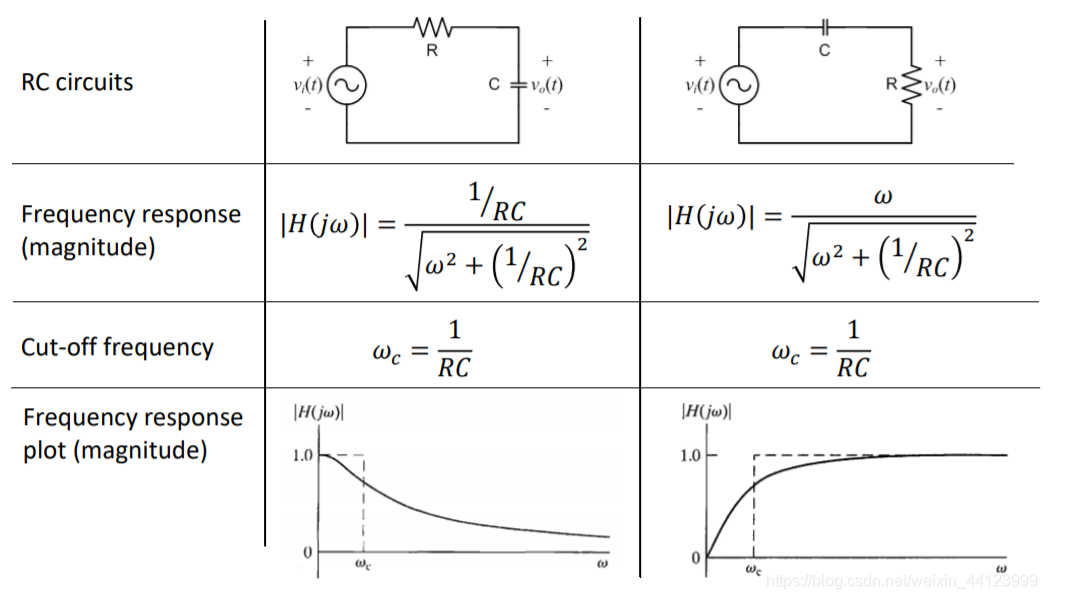
Figure 5: Diagramme de circuit de la série RC et formule de fréquence
Dans un circuit de la série RC, l'interaction entre la résistance (R) Et le condensateur (C) influence à la fois le flux de courant et la distribution de tension.Le rôle principal de la résistance est de réguler le flux de courant.Cette relation est quantifiée par la loi d'Ohm, qui indique 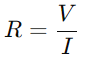 , où V est la tension et je est le courant.Essentiellement, la résistance agit comme un goulot d'étranglement, contrôlant la quantité d'électricité peut passer à tout moment.
, où V est la tension et je est le courant.Essentiellement, la résistance agit comme un goulot d'étranglement, contrôlant la quantité d'électricité peut passer à tout moment.
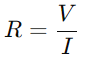 , où V est la tension et je est le courant.Essentiellement, la résistance agit comme un goulot d'étranglement, contrôlant la quantité d'électricité peut passer à tout moment.
, où V est la tension et je est le courant.Essentiellement, la résistance agit comme un goulot d'étranglement, contrôlant la quantité d'électricité peut passer à tout moment.La fonction du condensateur est légèrement plus complexe car elle stocke temporairement l'énergie électrique, puis la rejette dans le circuit.La tension à travers le condensateur (VC) est en corrélation avec sa charge stockée (Q) et est calculé à l'aide de la formule 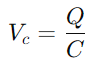 .Cette relation met en évidence la capacité du condensateur à maintenir la charge, impactant directement la tension qu'elle présente.Pendant le fonctionnement, la dynamique de la charge et de la décharge du condensateur est vitale pour comprendre les circuits RC.La constante de temps (τ), défini comme
.Cette relation met en évidence la capacité du condensateur à maintenir la charge, impactant directement la tension qu'elle présente.Pendant le fonctionnement, la dynamique de la charge et de la décharge du condensateur est vitale pour comprendre les circuits RC.La constante de temps (τ), défini comme 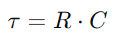 , mesure à quelle vitesse le condensateur atteint environ 63,2% de la tension complète fournie par la source (V0).Cette constante de temps indique comment le circuit s'adapte aux changements d'entrée, les propriétés de résistance et de condensateur dictant le rythme de ces ajustements.
, mesure à quelle vitesse le condensateur atteint environ 63,2% de la tension complète fournie par la source (V0).Cette constante de temps indique comment le circuit s'adapte aux changements d'entrée, les propriétés de résistance et de condensateur dictant le rythme de ces ajustements.
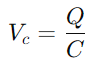 .Cette relation met en évidence la capacité du condensateur à maintenir la charge, impactant directement la tension qu'elle présente.Pendant le fonctionnement, la dynamique de la charge et de la décharge du condensateur est vitale pour comprendre les circuits RC.La constante de temps (τ), défini comme
.Cette relation met en évidence la capacité du condensateur à maintenir la charge, impactant directement la tension qu'elle présente.Pendant le fonctionnement, la dynamique de la charge et de la décharge du condensateur est vitale pour comprendre les circuits RC.La constante de temps (τ), défini comme 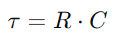 , mesure à quelle vitesse le condensateur atteint environ 63,2% de la tension complète fournie par la source (V0).Cette constante de temps indique comment le circuit s'adapte aux changements d'entrée, les propriétés de résistance et de condensateur dictant le rythme de ces ajustements.
, mesure à quelle vitesse le condensateur atteint environ 63,2% de la tension complète fournie par la source (V0).Cette constante de temps indique comment le circuit s'adapte aux changements d'entrée, les propriétés de résistance et de condensateur dictant le rythme de ces ajustements.La tension à travers le condensateur à tout moment donné pendant la charge est donnée par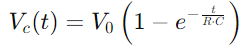 , illustrant une augmentation non linéaire lorsque le condensateur se remplit.Cette équation décrit comment le taux de charge ralentit à mesure que le condensateur aborde la pleine capacité.
, illustrant une augmentation non linéaire lorsque le condensateur se remplit.Cette équation décrit comment le taux de charge ralentit à mesure que le condensateur aborde la pleine capacité.
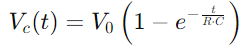 , illustrant une augmentation non linéaire lorsque le condensateur se remplit.Cette équation décrit comment le taux de charge ralentit à mesure que le condensateur aborde la pleine capacité.
, illustrant une augmentation non linéaire lorsque le condensateur se remplit.Cette équation décrit comment le taux de charge ralentit à mesure que le condensateur aborde la pleine capacité.Inversement, pendant la décharge, la tension du condensateur diminue en fonction de 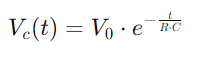 , décrivant une diminution linéaire de l'énergie stockée au fil du temps.Ce processus fournit une image claire de la façon dont l'énergie est libérée du condensateur dans le circuit.Dans les applications AC, la différence de phase entre la tension et le courant, φ, devient critique.Cette différence, calculée comme
, décrivant une diminution linéaire de l'énergie stockée au fil du temps.Ce processus fournit une image claire de la façon dont l'énergie est libérée du condensateur dans le circuit.Dans les applications AC, la différence de phase entre la tension et le courant, φ, devient critique.Cette différence, calculée comme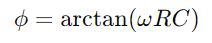 où Ω représente la fréquence angulaire, montre le retard causé par le condensateur, qui affecte la synchronisation entre lorsque les flux de courant et les changements de tension à travers les composants.
où Ω représente la fréquence angulaire, montre le retard causé par le condensateur, qui affecte la synchronisation entre lorsque les flux de courant et les changements de tension à travers les composants.
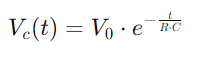 , décrivant une diminution linéaire de l'énergie stockée au fil du temps.Ce processus fournit une image claire de la façon dont l'énergie est libérée du condensateur dans le circuit.Dans les applications AC, la différence de phase entre la tension et le courant, φ, devient critique.Cette différence, calculée comme
, décrivant une diminution linéaire de l'énergie stockée au fil du temps.Ce processus fournit une image claire de la façon dont l'énergie est libérée du condensateur dans le circuit.Dans les applications AC, la différence de phase entre la tension et le courant, φ, devient critique.Cette différence, calculée comme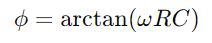 où Ω représente la fréquence angulaire, montre le retard causé par le condensateur, qui affecte la synchronisation entre lorsque les flux de courant et les changements de tension à travers les composants.
où Ω représente la fréquence angulaire, montre le retard causé par le condensateur, qui affecte la synchronisation entre lorsque les flux de courant et les changements de tension à travers les composants.Dans l'ensemble, la résistance limite et dirige l'écoulement du courant tandis que le condensateur stocke et module la tension.Ensemble, ils déterminent les caractéristiques de réponse du circuit, telles que la rapidité avec laquelle il peut charger et se décharger et les déphasages qui se produisent dans des scénarios de courant alternatifs.Ce comportement combiné sous-tend les opérations fondamentales des circuits de la série RC, ce qui les fait faire partie intégrante de diverses applications électroniques.
Équations de base du circuit de la série RC
Pour comprendre le comportement d'un circuit de la série RC, il est crucial de commencer par les équations de base qui décrivent sa réponse aux changements de tension d'entrée.Supposons que nous ayons une tension d'entrée changeante représentée comme Vin), avec la tension à travers la résistance étiquetée comme VR (T) et à travers le condensateur comme VC (T).Dans un circuit de série, le même courant, Il) traverse à la fois la résistance et le condensateur.
En appliquant la loi de tension de Kirchhoff (KVL), qui indique que la tension totale autour de toute boucle fermée dans un circuit doit être égale à zéro, nous constatons que la tension d'entrée est égale à la somme des tensions à travers la résistance et le condensateur:
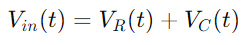
La tension à travers la résistance peut être calculée à l'aide de la loi d'Ohm:
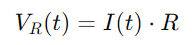
Pour le condensateur, la tension VC (t) est liée à la charge Q (t) qu'il détient, donnée par:
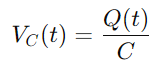
Étant donné que le courant est défini comme le débit de charge de charge, nous avons:

En substituant Q (t) dans l'équation pour VC (T)et en utilisant le dérivé de charge Il), nous dérivons l'équation différentielle de base pour le circuit de la série RC:
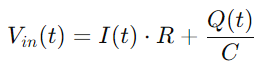
Remplacement supplémentaire Q (t) avec l'intégrale de Il), nous obtenons:
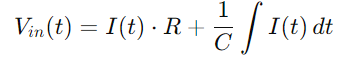
Pour le courant i (t), compte tenu du taux de variation de tension à travers le condensateur, nous utilisons:
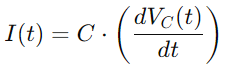
L'intégration de toutes ces relations nous donne l'équation différentielle décrivant la tension à travers le condensateur:
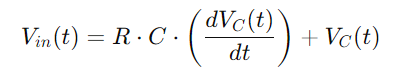
Il s'agit d'une équation différentielle linéaire de premier ordre qui capture le changement de tension en fonction du temps à travers le condensateur.La résolution de cette équation nous permet de décrire avec précision comment la tension du condensateur évolue.Cette compréhension est fondamentale pour analyser à la fois les cycles de charge et de décharge du condensateur, ainsi que la réponse du circuit à différentes fréquences.Cette approche complète donne un aperçu approfondi des caractéristiques dynamiques du circuit de la série RC.
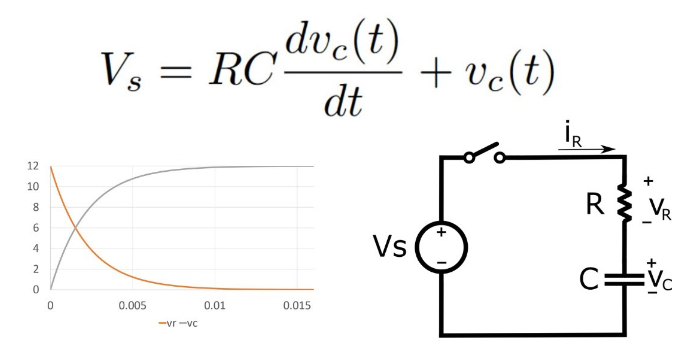
Figure 6: Équation différentielle de tension
Impédance du circuit de la série RC
Pour réécrire la description d'un circuit de la série RC, en mettant l'accent sur l'interaction humaine et une explication directe et simplifiée, améliorons les expériences tangibles et les opérations étape par étape impliquées tout en maintenant le message de base et la cohérence:
Dans un circuit de la série RC, la résistance et le condensateur fonctionnent en tandem pour contrôler le flux d'électricité, crucial lorsqu'il s'agit de courants alternés.L'impédance totale du circuit, représentée comme 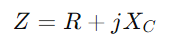 , combine la résistance R et la réactance capacitive xc.La caractéristique clé de cette configuration est que les valeurs d'impédance pour les deux composants varient avec les changements de fréquence.À mesure que la fréquence augmente, l'impédance du condensateur diminue, permettant à plus de courant de passer, tandis que la résistance reste essentiellement constante.
, combine la résistance R et la réactance capacitive xc.La caractéristique clé de cette configuration est que les valeurs d'impédance pour les deux composants varient avec les changements de fréquence.À mesure que la fréquence augmente, l'impédance du condensateur diminue, permettant à plus de courant de passer, tandis que la résistance reste essentiellement constante.
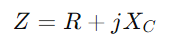 , combine la résistance R et la réactance capacitive xc.La caractéristique clé de cette configuration est que les valeurs d'impédance pour les deux composants varient avec les changements de fréquence.À mesure que la fréquence augmente, l'impédance du condensateur diminue, permettant à plus de courant de passer, tandis que la résistance reste essentiellement constante.
, combine la résistance R et la réactance capacitive xc.La caractéristique clé de cette configuration est que les valeurs d'impédance pour les deux composants varient avec les changements de fréquence.À mesure que la fréquence augmente, l'impédance du condensateur diminue, permettant à plus de courant de passer, tandis que la résistance reste essentiellement constante.L'impédance, désignée comme Z et mesuré en ohms (ω), joue un rôle essentiel dans la détermination de la réaction du circuit au courant alternatif.Comme dans les circuits de la série RL, la résistance R et réactance capacitive xC d'un circuit RC forment un triangle connu sous le nom de triangle d'impédance.Ce triangle se rapporte étroitement au triangle de tension, et en appliquant le théorème de Pythagore, vous pouvez calculer l'impédance totale du circuit.
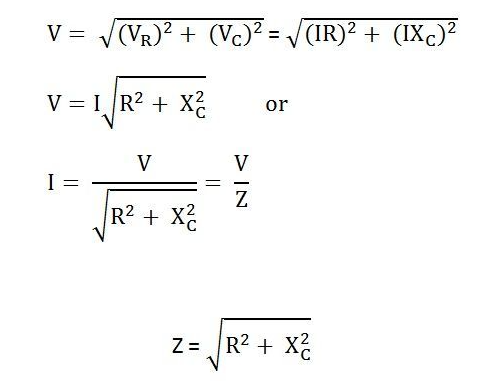
Figure 7: Formule de calcul du circuit de la série RC
En ce qui concerne les applications pratiques, considérez les écouteurs, qui utilisent ces principes.Les écouteurs à haute impédance, dépassant souvent 200 ohms, sont généralement utilisés avec des ordinateurs de bureau, des amplificateurs de puissance et des équipements audio professionnels.Ces modèles à haute impédance correspondent bien aux capacités de sortie de l'électronique de qualité professionnelle.Lorsque vous utilisez ces écouteurs, il est crucial de régler progressivement le volume pour éviter la surcharge et les dommages des composants internes délicats, tels que la bobine vocale.
À l'inverse, les écouteurs à faible impédance, généralement inférieurs à 50 ohms, sont préférés pour des appareils portables comme les lecteurs de CD, les lecteurs MD ou les lecteurs MP3.Ces écouteurs nécessitent moins d'électricité pour offrir un audio de haute qualité, ce qui les rend idéaux pour une utilisation mobile.Cependant, ils nécessitent également une attention particulière aux niveaux de sensibilité pour garantir des performances optimales et éviter les dommages aux écouteurs ou en audition.
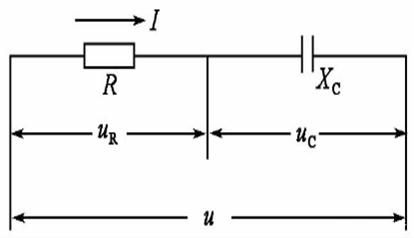
Figure 8: Diagramme d'impédance du circuit de la série RC
Procédures d'admission et d'analyse des circuits de la série RC
L'admission mesure la facilité avec laquelle un circuit de la série RC peut conduire de l'électricité, calculé comme l'inverse de l'impédance (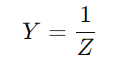 ).Cette valeur intègre à la fois la résistance (R) et la réactance (X) du circuit.La résistance s'oppose au flux de courant en convertissant l'énergie électrique en chaleur, tandis que la réactance stocke l'énergie temporairement dans le circuit.
).Cette valeur intègre à la fois la résistance (R) et la réactance (X) du circuit.La résistance s'oppose au flux de courant en convertissant l'énergie électrique en chaleur, tandis que la réactance stocke l'énergie temporairement dans le circuit.
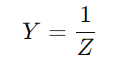 ).Cette valeur intègre à la fois la résistance (R) et la réactance (X) du circuit.La résistance s'oppose au flux de courant en convertissant l'énergie électrique en chaleur, tandis que la réactance stocke l'énergie temporairement dans le circuit.
).Cette valeur intègre à la fois la résistance (R) et la réactance (X) du circuit.La résistance s'oppose au flux de courant en convertissant l'énergie électrique en chaleur, tandis que la réactance stocke l'énergie temporairement dans le circuit.Pour calculer l'admission
Commencez par écrire l'impédance 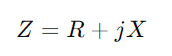 , où r signifie résistance, X pour la réactance, et J est l'unité imaginaire.Utilisez la formule y = 1 / (R + jx).Cette opération implique des nombres complexes et nous donne
, où r signifie résistance, X pour la réactance, et J est l'unité imaginaire.Utilisez la formule y = 1 / (R + jx).Cette opération implique des nombres complexes et nous donne 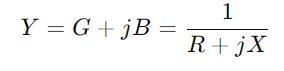 .Ici, G est la conductance (capacité d'écoulement actuelle réelle) et B est la sensibilité (la capacité du circuit à réagir aux changements de courant).
.Ici, G est la conductance (capacité d'écoulement actuelle réelle) et B est la sensibilité (la capacité du circuit à réagir aux changements de courant).
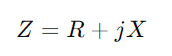 , où r signifie résistance, X pour la réactance, et J est l'unité imaginaire.Utilisez la formule y = 1 / (R + jx).Cette opération implique des nombres complexes et nous donne
, où r signifie résistance, X pour la réactance, et J est l'unité imaginaire.Utilisez la formule y = 1 / (R + jx).Cette opération implique des nombres complexes et nous donne 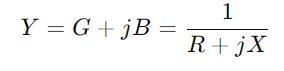 .Ici, G est la conductance (capacité d'écoulement actuelle réelle) et B est la sensibilité (la capacité du circuit à réagir aux changements de courant).
.Ici, G est la conductance (capacité d'écoulement actuelle réelle) et B est la sensibilité (la capacité du circuit à réagir aux changements de courant).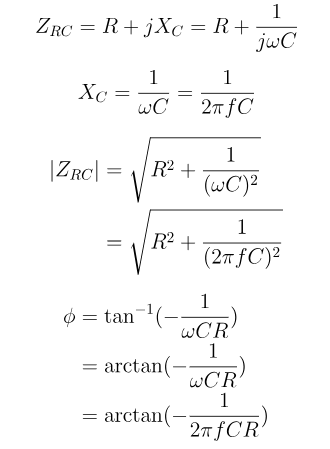
Figure 9: calculatrice d'impédance du circuit de la série RC
Ce calcul révèle non seulement la conductivité du circuit, mais aussi ses caractéristiques de réponse dynamique, cruciale pour l'analyse du circuit AC.La conductance et la sensibilité, prises ensemble, indiquent comment le circuit passe le courant et comment il stocke et libère de l'énergie.
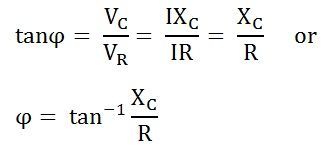
Figure 10: Formule d'angle de phase
Application pratique
Les ingénieurs utilisent des valeurs d'admission pour améliorer la conception des circuits, en particulier dans les applications à haute fréquence telles que les circuits radiofréquences.L'ajustement de l'admission aide à l'appariement de l'impédance, à la réduction de la réflexion du signal et à l'amélioration de l'efficacité de transmission.
En étudiant la réponse d'admission, les ingénieurs peuvent évaluer et prédire les performances du circuit dans diverses conditions comme la réponse en fréquence, la stabilité et la sensibilité.Équipez d'un oscilloscope et d'un générateur de signal pour mesurer la tension et le courant du circuit à des fréquences variables.Concentrez-vous en particulier sur la fréquence de coupure pour tester les prédictions théoriques et les valider contre les observations pratiques.Pour les circuits AC, commencez par déterminer la réactance (XC) du condensateur avec 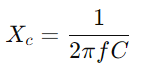 , où f est la fréquence du signal.Calculez l'impédance totale
, où f est la fréquence du signal.Calculez l'impédance totale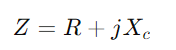 Et puis l'admission
Et puis l'admission 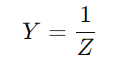 .
.
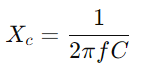 , où f est la fréquence du signal.Calculez l'impédance totale
, où f est la fréquence du signal.Calculez l'impédance totale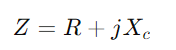 Et puis l'admission
Et puis l'admission 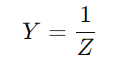 .
.Analyser la différence de phase en utilisant 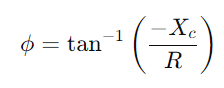 Pour comprendre l'altération de la forme du signal.Examinez comment le circuit gère différentes fréquences, notant en particulier le comportement à la fréquence de coupure
Pour comprendre l'altération de la forme du signal.Examinez comment le circuit gère différentes fréquences, notant en particulier le comportement à la fréquence de coupure  , où le circuit passe du passage aux signaux de blocage.L'évaluation de la façon dont l'impédance et la différence de phase varient avec la fréquence, est crucial pour la conception de filtres et de processeurs de signal efficaces.Discutez de la façon dont la sélectivité de fréquence, les déphasages et l'atténuation du signal en raison des propriétés du circuit affectent les applications pratiques comme le filtrage et le réglage électronique.
, où le circuit passe du passage aux signaux de blocage.L'évaluation de la façon dont l'impédance et la différence de phase varient avec la fréquence, est crucial pour la conception de filtres et de processeurs de signal efficaces.Discutez de la façon dont la sélectivité de fréquence, les déphasages et l'atténuation du signal en raison des propriétés du circuit affectent les applications pratiques comme le filtrage et le réglage électronique.
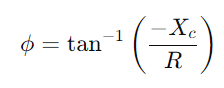 Pour comprendre l'altération de la forme du signal.Examinez comment le circuit gère différentes fréquences, notant en particulier le comportement à la fréquence de coupure
Pour comprendre l'altération de la forme du signal.Examinez comment le circuit gère différentes fréquences, notant en particulier le comportement à la fréquence de coupure  , où le circuit passe du passage aux signaux de blocage.L'évaluation de la façon dont l'impédance et la différence de phase varient avec la fréquence, est crucial pour la conception de filtres et de processeurs de signal efficaces.Discutez de la façon dont la sélectivité de fréquence, les déphasages et l'atténuation du signal en raison des propriétés du circuit affectent les applications pratiques comme le filtrage et le réglage électronique.
, où le circuit passe du passage aux signaux de blocage.L'évaluation de la façon dont l'impédance et la différence de phase varient avec la fréquence, est crucial pour la conception de filtres et de processeurs de signal efficaces.Discutez de la façon dont la sélectivité de fréquence, les déphasages et l'atténuation du signal en raison des propriétés du circuit affectent les applications pratiques comme le filtrage et le réglage électronique.Cette approche décompose les processus opérationnels en étapes gérables, enrichissant la compréhension de l'utilisateur avec des informations pratiques sur la manipulation et l'analyse des circuits de la série RC.
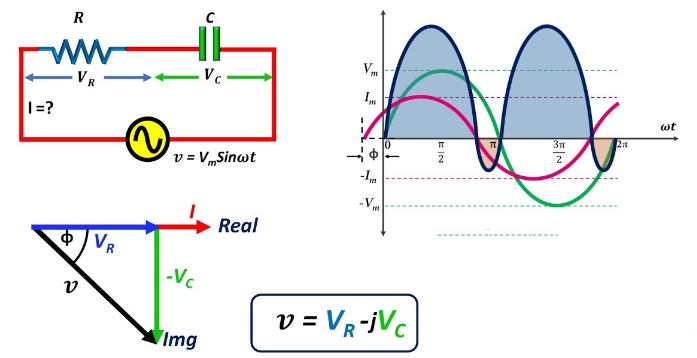
Figure 11: Caractéristiques des circuits de la série RC
Diagramme de phaseur du circuit de la série RC
Dans un circuit de la série RC, tous les éléments partagent le même courant en raison de leur configuration de série.Ce courant uniforme agit comme une base de référence pour notre diagramme de phaseur, qui aide à visualiser la relation entre différentes tensions et courants dans le circuit.Désignons ce courant je comme phaseur de référence, positionné à zéro degrés sur le diagramme.Dans le diagramme, le courant je est réglé horizontalement vers la droite, établissant la ligne de référence à zéro degré.La tension à travers la résistance (UR) est en phase avec le courant car les résistances ne provoquent aucun décalage de phase.Ainsi, UR est dessiné comme un vecteur horizontal dans la même direction que je, s'étendant de l'origine.
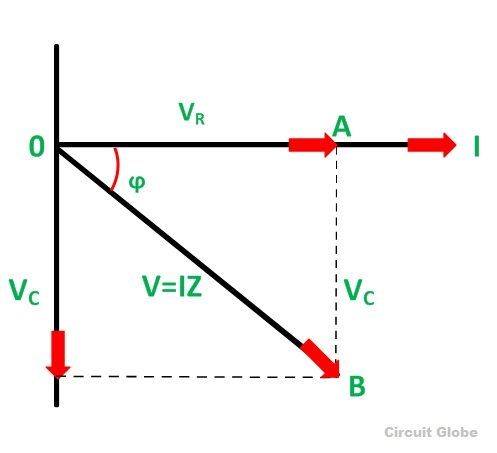
Figure 12: Diagramme de phaseur du circuit de la série RC
En revanche, la tension à travers le condensateur (UC) conduit le courant de 90 degrés en raison de la propriété capacitive de retard de la phase actuelle.Cette tension est représentée par un vecteur vertical pointant vers le haut, à partir de la pointe du UR vecteur.La tension totale U dans le circuit est la somme vectorielle de U Rand UC.Cette somme forme un triangle droit avec UR et UC comme les côtés adjacents et opposés, respectivement.L'hypoténuse de ce triangle, s'étendant de l'origine à la pointe du UC vecteur, représente U.
Le courant sinusoïdal à travers le circuit est donné par le péché (Ωt), où im est l'amplitude de courant maximale et Ω est la fréquence angulaire.Par conséquent, la tension à travers la résistance est 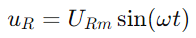 , reflétant la forme d'onde de courant.La tension à travers le condensateur est donnée par
, reflétant la forme d'onde de courant.La tension à travers le condensateur est donnée par 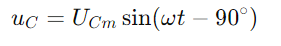 , indiquant un décalage de phase de -90 ° (ou 90 degrés devant le courant).Le triangle droit du diagramme du phaseur clarifie que
, indiquant un décalage de phase de -90 ° (ou 90 degrés devant le courant).Le triangle droit du diagramme du phaseur clarifie que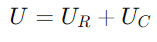 n'est pas seulement en amplitude mais aussi en relation de phase, avec le vecteur de tension terminal (U) terminer le triangle.
n'est pas seulement en amplitude mais aussi en relation de phase, avec le vecteur de tension terminal (U) terminer le triangle.
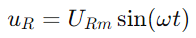 , reflétant la forme d'onde de courant.La tension à travers le condensateur est donnée par
, reflétant la forme d'onde de courant.La tension à travers le condensateur est donnée par 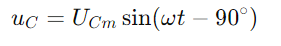 , indiquant un décalage de phase de -90 ° (ou 90 degrés devant le courant).Le triangle droit du diagramme du phaseur clarifie que
, indiquant un décalage de phase de -90 ° (ou 90 degrés devant le courant).Le triangle droit du diagramme du phaseur clarifie que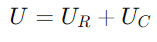 n'est pas seulement en amplitude mais aussi en relation de phase, avec le vecteur de tension terminal (U) terminer le triangle.
n'est pas seulement en amplitude mais aussi en relation de phase, avec le vecteur de tension terminal (U) terminer le triangle.
Figure 13: Diagramme de phaseur de tension du circuit de la série RC
Points clés dans l'analyse des circuits RC de la série
Impédance dans le circuit de la série RC, représentée comme Z, combine la résistance (R) et l'effet réactif de la capacité en une seule mesure qui varie avec la fréquence du signal.Il s'exprime mathématiquement comme 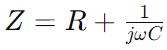 , où Ω est la fréquence angulaire et C est la capacité.Ici, R constitue la réelle partie de l'impédance et
, où Ω est la fréquence angulaire et C est la capacité.Ici, R constitue la réelle partie de l'impédance et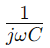 représente la partie imaginaire, indiquant comment le condensateur influence le circuit.
représente la partie imaginaire, indiquant comment le condensateur influence le circuit.
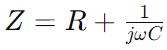 , où Ω est la fréquence angulaire et C est la capacité.Ici, R constitue la réelle partie de l'impédance et
, où Ω est la fréquence angulaire et C est la capacité.Ici, R constitue la réelle partie de l'impédance et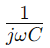 représente la partie imaginaire, indiquant comment le condensateur influence le circuit.
représente la partie imaginaire, indiquant comment le condensateur influence le circuit.La façon dont l'impédance change avec la fréquence est essentielle pour utiliser les circuits RC série dans les applications de filtrage.À des fréquences plus basses, le circuit présente une impédance plus élevée, bloquant efficacement ces fréquences.Inversement, à des fréquences plus élevées, l'impédance baisse, permettant à ces fréquences de passer plus librement.Ce comportement rend les circuits RC en série idéaux pour les tâches telles que le filtrage du bruit à basse fréquence indésirable ou le passage des signaux à haute fréquence.
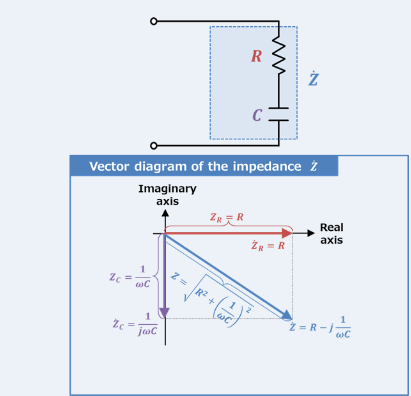
Figure 14: Diagramme de vecteur d'impédance du circuit de la série RC
Conclusion
Du filtrage des fréquences indésirables à la mise en forme des réponses du signal, le circuit de la série RC est déterminant dans une large gamme de fonctions électroniques.En comprenant les principes sous-jacents tels que l'impédance, les relations de phaseur et le comportement dépendant de la fréquence de ces circuits, les ingénieurs et les concepteurs sont équipés pour élaborer des solutions qui gèrent efficacement l'intégrité du signal dans les systèmes électroniques complexes.L'examen détaillé de ces circuits, soutenu par l'analyse mathématique et les représentations visuelles comme les diagrammes de phases, offre un aperçu complet qui est important pour tous ceux qui cherchent à approfondir leur compréhension de la dynamique électronique des circuits ou pour améliorer leurs compétences pratiques en matière de conception de circuits et de dépannage.
Questions fréquemment posées [FAQ]
1. Quel est le principe du circuit RC?
Le principe d'un circuit RC (résistance-condensateur) tourne autour des processus de charge et de décharge du condensateur à travers la résistance.Dans ce circuit, la capacité du condensateur à stocker et à libérer l'énergie électrique interagit avec la résistance, qui contrôle la vitesse à laquelle le condensateur charge ou décharge.
2. Pourquoi un circuit RC est-il en cours de courant?
Dans un circuit RC, le courant mène la tension à travers le condensateur car le condensateur doit commencer à charger avant que sa tension ne puisse augmenter.Étant donné que le courant s'écoule dans le condensateur pour le charger, le courant culmine avant que la tension à travers le condensateur atteigne son maximum.Cet effet provoque un décalage de phase où la phase actuelle entraîne la phase de tension jusqu'à 90 degrés, selon la fréquence du signal d'entrée.
3. Comment la tension change-t-elle dans un circuit RC?
Le changement de tension dans un circuit RC pendant la charge est décrit par une fonction exponentielle.Lorsqu'une tension est appliquée, la tension à travers le condensateur augmente initialement rapidement, puis ralentit à l'approche de la tension d'alimentation.Mathématiquement, cela s'exprime comme 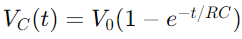 , où VC(t) La tension à travers le condensateur au temps t, V0 est la tension d'alimentation, et RC est la constante de temps du circuit, déterminant la rapidité avec laquelle le condensateur charge.Inversement, lors de la décharge, la tension à travers le condensateur diminue de façon exponentielle, après l'équation
, où VC(t) La tension à travers le condensateur au temps t, V0 est la tension d'alimentation, et RC est la constante de temps du circuit, déterminant la rapidité avec laquelle le condensateur charge.Inversement, lors de la décharge, la tension à travers le condensateur diminue de façon exponentielle, après l'équation 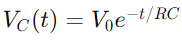 .
.
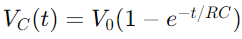 , où VC(t) La tension à travers le condensateur au temps t, V0 est la tension d'alimentation, et RC est la constante de temps du circuit, déterminant la rapidité avec laquelle le condensateur charge.Inversement, lors de la décharge, la tension à travers le condensateur diminue de façon exponentielle, après l'équation
, où VC(t) La tension à travers le condensateur au temps t, V0 est la tension d'alimentation, et RC est la constante de temps du circuit, déterminant la rapidité avec laquelle le condensateur charge.Inversement, lors de la décharge, la tension à travers le condensateur diminue de façon exponentielle, après l'équation 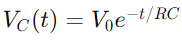 .
. À PROPOS DE NOUS
Satisfaction client à chaque fois.Confiance mutuelle et intérêts communs.
À PROPOS DE NOUS
Satisfaction client à chaque fois.Confiance mutuelle et intérêts communs.
test de fonctionnalité.Les produits les plus rentables et le meilleur service sont notre engagement éternel.
Article chaud
- Sont CR2032 et CR2016 interchangeables
- MOSFET: Définition, principe de travail et sélection
- Installation et test de relais, interprétation des schémas de câblage de relais
- CR2016 contre CR2032 Quelle est la différence
- NPN contre PNP: Quelle est la différence?
- ESP32 vs STM32: Quel microcontrôleur est meilleur pour vous?
- LM358 Double amplificateur opérationnel Guide complet: broches, diagrammes de circuits, équivalents, exemples utiles
- CR2032 VS DL2032 VS CR2025 Guide de comparaison
- Comprendre les différences ESP32 et ESP32-S3 Analyse technique et de performance
- Analyse détaillée du circuit de la série RC
 Analyse approfondie des diodes 1N4148: modes de fonctionnement, spécifications et scénarios d'utilisation
Analyse approfondie des diodes 1N4148: modes de fonctionnement, spécifications et scénarios d'utilisation
2024-05-08
 Comprendre les types et les utilisations des pompes de déplacement dynamiques et positives
Comprendre les types et les utilisations des pompes de déplacement dynamiques et positives
2024-05-07
Numéro de pièce chaud
 C3216JB2J472M115AA
C3216JB2J472M115AA GCM2165C2A151JA16D
GCM2165C2A151JA16D GRM31CR71C475MA01L
GRM31CR71C475MA01L C0603C0G1E5R1B030BG
C0603C0G1E5R1B030BG TMK063CH220JT-F
TMK063CH220JT-F 0805YC152JAT2A
0805YC152JAT2A GCM3195C2A272JA16D
GCM3195C2A272JA16D GCM3195C2A432JA16D
GCM3195C2A432JA16D LD02YC182JAB2A
LD02YC182JAB2A GQM1555C2D2R8BB01D
GQM1555C2D2R8BB01D
- 1812AC473KAT2A
- 0805YA332JA12A
- GRM0335C1H8R3CD01D
- VS-6F60
- CY7C68013-100AXC
- DG406DW-E3
- DG407DN
- SLA6868MZ
- RT0805BRD07102KL
- MK40DX128VLH7
- CY7C144AV-25AC
- V24C15C100BG
- PM15CTM060-11
- PM900HS060
- AD5259BRMZ50
- TPS65217BRSLT
- T495B106M010ZTE750
- AD5232BRU50
- FDP050AN06A0
- MC33269DTRK-5.0G
- HY11P41-E016-014
- IDT70914S12PF
- M306V7MG-155FP
- MAX847EEI
- MB90F867ASPF
- MT52L256M64D2GN-107WT:B
- PF38F4050L0YBQ2
- R5F3640MDFB
- SAF-XE167FM-72F80L
- TPIC1346DBTRG4
- INMP441ACEZ
- E86D-0413B
- HD74HC574RPEL
- LV3130V-TLM-E
- N7600060FKC101
- UPD77642BF1-GA9-A
- STPCV1KEBI
- BU7213AKVT
- HY5S5B6ELF-SEDR